初识递归

view times

什么是递归

一个函数调用本身就是递归。
递归和普通函数调用一样，是通过栈实现的。

递归的条件

  • 一个问题的解可以分解为几个子问题的解
  • 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
  • 存在递归终止条件

递归的作用

  • 代替多重循环
  • 解决本来就是用递归形式定义的问题
  • 将问题分解为规模更小的子问题进行求解

写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，再推敲出终止条件，最后将递推公式和终止条件翻译成代码。

不要试图想清楚整个递和归的过程，这样容易被绕进去。

编写递归代码的关键是，只要遇到递归，我们就把它抽象成一个递推公式, 不用想一层层的调用关系，不要试图用人脑去分解递归的整个步骤。

注意事项

递归代码要警惕栈溢出

如果递归求解的数据规模很大，调用层次很深，一直压入栈，就会有栈溢出的风险。

递归代码要警惕重复计算

重复计算就是 f(k) 被计算多次，影响效率。
可以用数据结构（比如散列表），来保存已经求解过的 f(k)。

在计算斐波那契函数 F(n) 的过程中， 我们可以使用 哈希表 来跟踪每个以 n 为键的 F(n) 的结果。 散列表 作为一个缓存，可以避免重复计算。 记忆化技术 是一个很好的例子，它演示了如何通过增加额外的空间以减少计算时间。

函数可能会有多个位置进行自我调用

递归的复杂度

时间复杂度：

递归中函数调用较多，执行所需时间也比较多。
给出一个递归算法，其时间复杂度 O ( T ) 通常是 递归调用的数量 (记作 R) 和单次计算的时间复杂度 (表示为 O ( S ) )的乘积。

1
O(T)=R∗O(s)

一般情况下单次计算的时间复杂度为 O ( 1 )

执行树

执行树 是一个用于表示递归函数的执行流程的树。树中的每个节点都表示递归函数的调用。因此，树中的节点总数对应于执行期间的递归调用的数量。

归函数的执行树将形成 n 叉树，其中 n 作为递推关系中出现递归的次数。例如，斐波那契函数的执行将形成二叉树，下面的图示展现了用于计算斐波纳契数 f(4) 的执行树。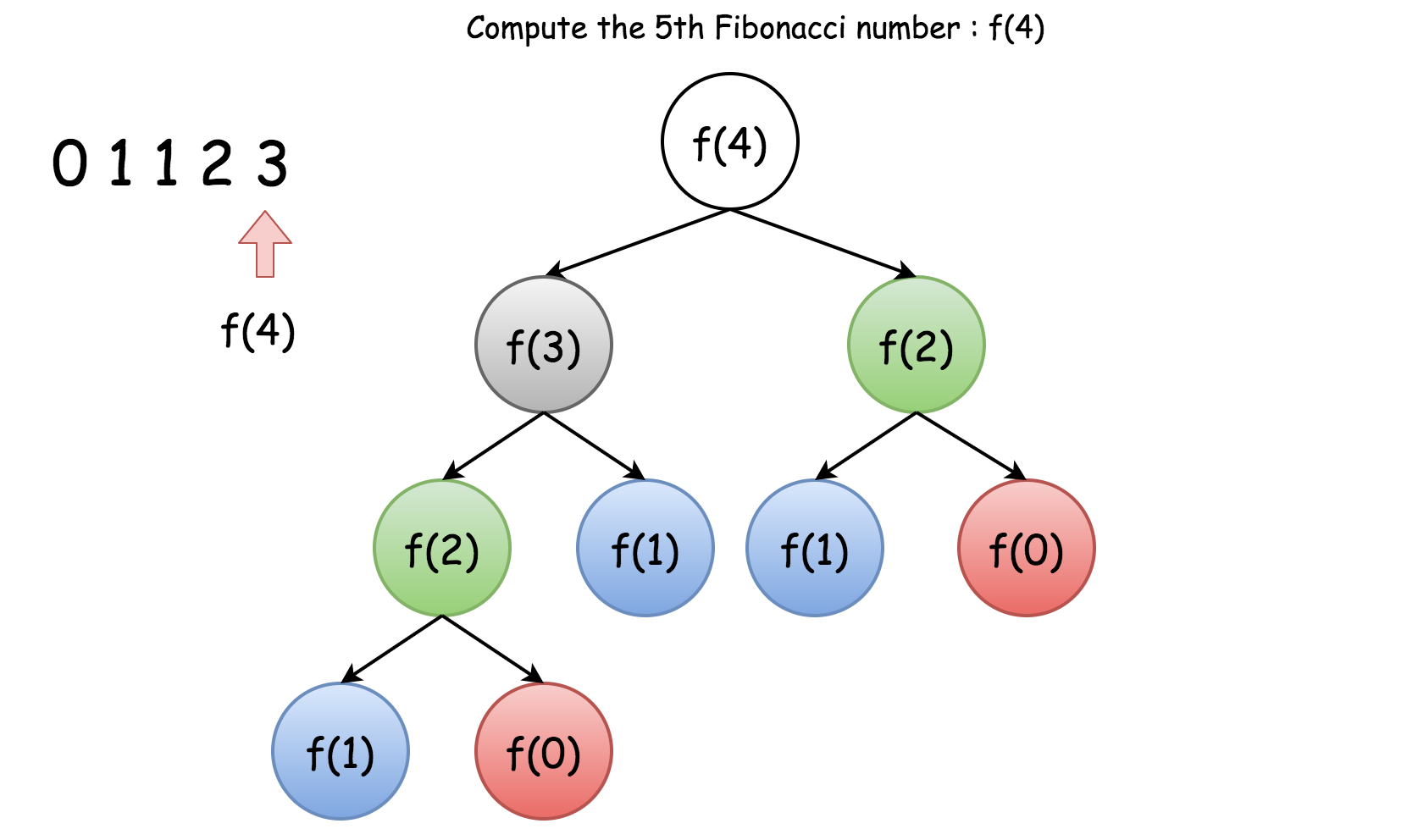
image

在 n 层的完全二叉树中，节点的总数为 2^n -1 。因此 f(n) 中递归数目的上限（尽管不严格）也是 2^n -1。那么我们可以估计 f(n) 的时间复杂度为 O(2^n)。

通过使用 记忆化技术 计算 f(n) 的递归将被调用 n-1 次以计算它所依赖的所有先验数字。

此时时间复杂度为: O ( 1 ) * n = O ( n )。记忆化技术不仅可以优化算法的时间复杂度，还可以简化时间复杂度的计算。

空间复杂度：

在计算递归算法的空间复杂度时，应该考虑造成空间消耗的两个部分：递归相关空间（recursion related space）和 非递归相关空间（non-recursion related space）。

非递归相关空间

递归相关空间是指由递归直接引起的内存开销，即用于跟踪递归函数调用的堆栈。
因为递归调用一次就会在内存栈中保存一次现场数据，所以在分析递归代码空间复杂度时，需要首先考虑这部分的开销。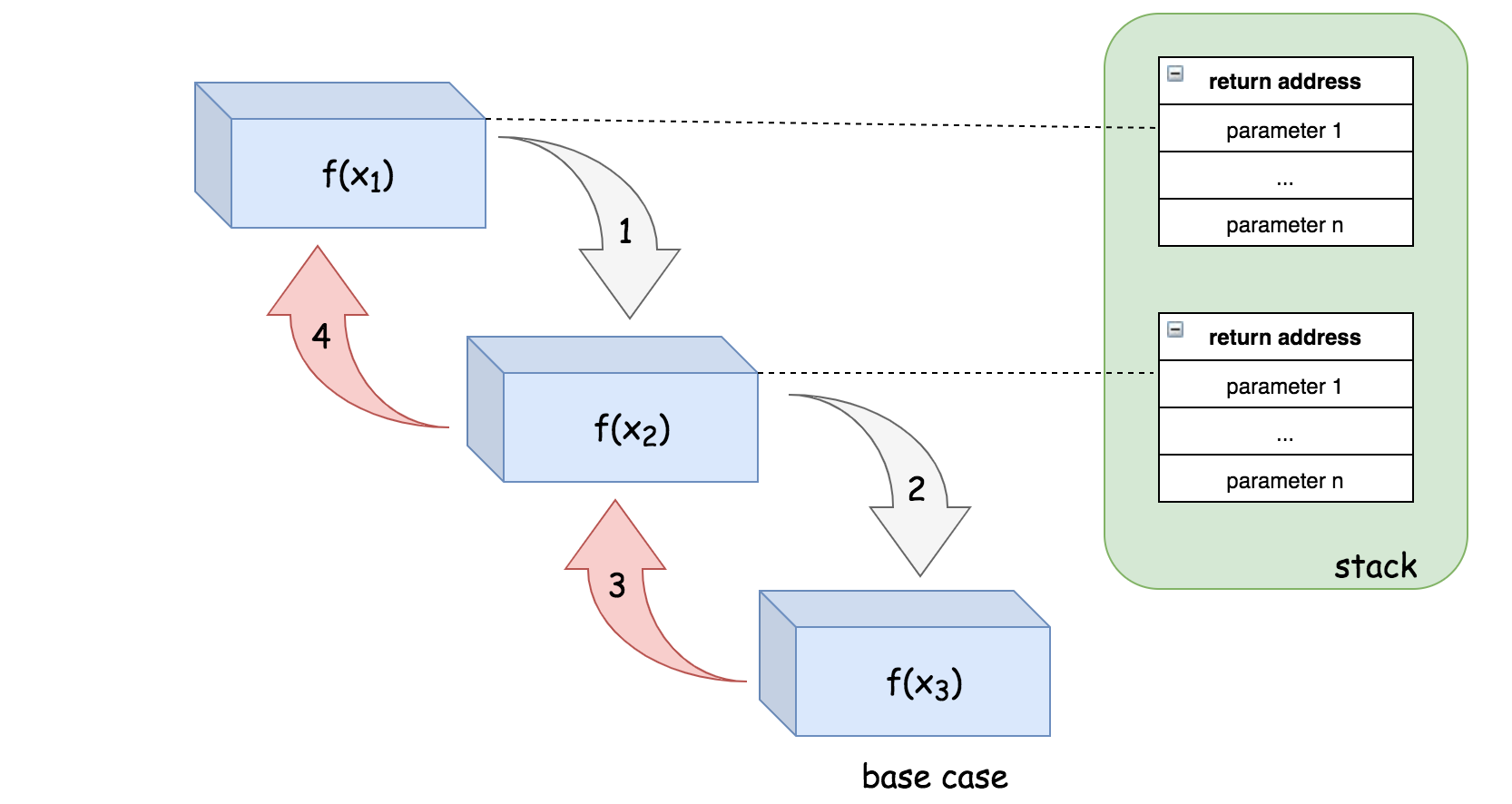
image

如果递归规模较大，可以自己模拟一个栈，用非递归的方法实现。因为递归借助的是我们看不到的系统栈，调用过多时系统栈会溢出。

递归相关空间

通常包括为全局变量分配的空间（通常在堆中）。
还可能包括使用 记忆化技术 时，保存递归调用的中间结果分配的空间。

尾递归

一般递归调用会在系统调用栈上产生的隐式额外空间。有一种然而，你应该学习识别一种称为尾递归的特殊递归情况，它不受此空间开销的影响。

尾递归函数是递归函数的一种，其中递归调用是递归函数中的最后一条指令。并且在函数中应该只有一次递归调用。

下面的打印字符串就是尾递归的一种情况，即递归调用之后就没有额外的计算语句了。

尾递归的好处是，它可以避免递归调用期间栈空间开销的累积，因为系统可以为每个递归调用重用栈中的固定空间。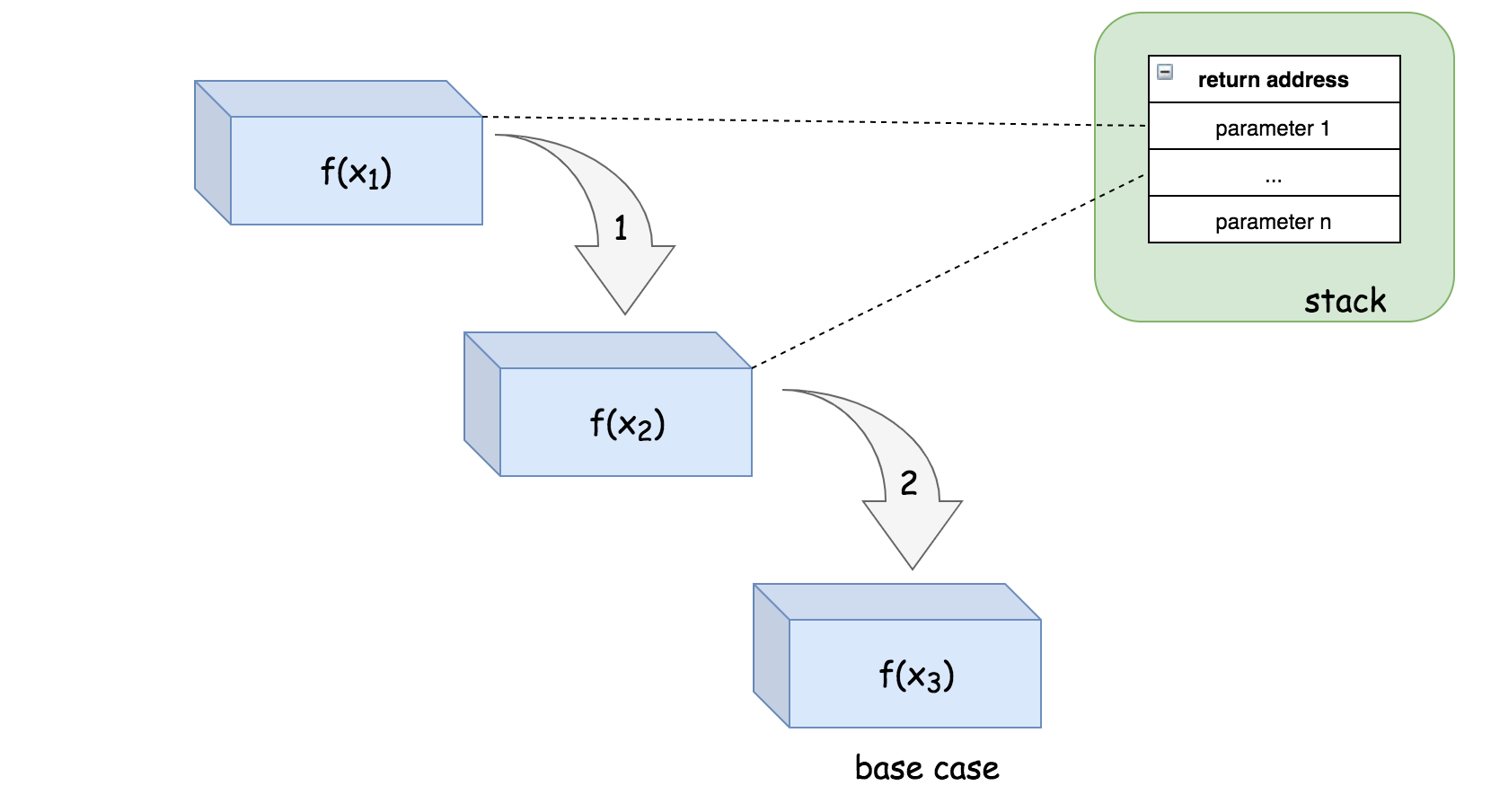
image

请注意，在尾递归的情况下，一旦从递归调用返回，我们也会立即返回，因此我们可以跳过整个递归调用返回链，直接返回到原始调用方。这意味着我们根本不需要所有递归调用的调用栈，这为我们节省了空间。

例如，在步骤（1）中，栈中的一个空间将被分配给 f(x1)，以便调用 f(x2)。然后，在步骤（2）中，函数 f(x2) 能够递归地调用 f(x3)，但是，系统不需要在栈上分配新的空间，而是可以简单地重用先前分配给第二次递归调用的空间。最后，在函数 f(x3) 中，我们达到了基本情况，该函数可以简单地将结果返回给原始调用方，而不会返回到之前的函数调用中。

总结

1、当我们面对一个问题，不清楚是否可以使用递归时，我们可以尝试写下递推关系式，利用数学公式来推导某些关系。

2、尽可能使用记忆化技术，减少重复计算

3、担心可能因为递归次数太多，而导致堆栈溢出时，可以使用尾递归。

一些帮助理解的题目

一、以相反的顺序打印字符串
首先，我们可以将所需的函数定义为 printReverse(str[0…n-1])，其中 str[0] 表示字符串中的第一个字符。然后我们可以分两步完成给定的任务：

首先，我们可以将所需的函数定义为 printReverse(str[0…n-1])，其中 str[0] 表示字符串中的第一个字符。然后我们可以分两步完成给定的任务：

  • printReverse(str[1…n-1])：以相反的顺序打印子字符串 str[1…n-1] 。
  • print(str[0])：打印字符串中的第一个字符。
1
2
3
4
5
6
7
void printReverse(const char *str) {
//函数首次传入的是 str 的首地址，也就是 &str[0]
  if (!*str)
    return; //在 str[n-1] = '\0' 时终止
  printReverse(str + 1);
  putchar(*str);
}

例题

汉诺塔可以看做递归问题
N 皇后问题其实是回溯问题

N皇后问题
每行只能放置一个皇后、每列也只能放置一个皇后。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>
#include <iostream>
#include <string>
#include <cmath>
#include <algorithm>
#include <cstdio>
#include <stack>
using namespace std;
 /*
 输出结果里的每一行都代表一种摆法。
 行里的第i个数字如果是n，就代表第i行的数字应该放在第n列。
 皇后的行、列编号都是从 1开始算。 
*/
int N;
int queenPos[100];
//用来存放算好的皇后位置。最左上角是 (0,0) 
void NQueen(int k){
	//在 0~k-1行已经摆好的情况下，摆第k行及其后面的元素
	int i;
	if(k==N){
		//N个皇后已经摆好
		for(i=0;i<N;i++)
			cout<<queenPos[i]+1<<" ";
		cout<<endl;
		return ; 
	} 
	for(i=0;i<N;i++){
		//逐尝试第k个皇后的位置
		int j;
		for(j=0;j<k;j++) {
			//和已经摆好的 k 个皇后的位置比较，看是否冲突
			if(queenPos[j] == i|| abs(queenPos[j]-i)==abs(k-j))
				break; 
				//第一个条件表示第 i 列已经有皇后了
				//第二个条件表示两个皇后是否在同一条对角斜线上 
		}
		if(j==k){
			//当前选的位置 i 不冲突
			queenPos[k] = i;
			//queenPos[k] 在第一次赋值后，回溯时值是可能会改变的。
			NQueen(k+1); 
		}
	//这是一个for循环中的递归，称作回溯。
	}//for循环终止
	
}

int main(int argc, char *argv[]) {
	cin>>N;
	NQueen(0);  
	//从第0行开始摆皇后
    return 0;
}

全排列

求 1~n 的全排列。可以分为若干个子问题：以 1 开头的全排列；以 2 开头的全排列；以 3 开头的全排列…

  • 数组 P 用来存放当前排列
  • 散列数组 hashTable[x] 当整数 x 已经在数组 P 中时为 true。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
const int maxn = 11;
// P为当前排列，hashTable 记录整数 x 是否已经在 P 中 
int n,P[maxn],hashTable[maxn] = {false};
// 当前处理排列的第 index 位
void generate(int index){
	if(index==n+1){ //递归边界,已经处理完排列的 n+1 位 
		for(int i=1;i<=n;i++)
			printf("%d",P[i]);
	printf("\n");
	return ;
	}
	for(int j=1;j<=n;j++){ //枚举 1~n，试图将 j 填入P[index]
		if(hashTable[j]==false){ // 如果 x 不在 P[0]~P[index-1]中 
			P[index]=j;           // 把 x 加入当前排列 
			hashTable[j]=true;    // 记 x 已在 P 中
			generate(index+1); 	  // 处理排列的第 index+1 位
			hashTable[j] = false; // 已处理完 P[index] 为 j 的子问题，还原状态 
		} 
	}
}
int main()
{
	n=3;   
	generate(1);  // 从 P [1] 开始填

	return 0;
}

回溯法实现 N 皇后

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void  generate(int index){
	if(index==n+1){  //递归边界 
		count++; //能达到这里的一定是合法的
		return; 
	}
	for(int x=1;x<=n;x++){  //第 x 行 
		if(hashTable[x]==false){ //第 x 行还没有皇后 
			bool flag = true; 
			for(int pre=1;pre<index;pre++){ //遍历之前的皇后 
				if(abs(index-pre) == abs(x-P[pre])){
					flag=false;
					break;
				}
			}
			if(flag){ //可以把皇后放在第 n 行 
				P[index]=x;
				hashTable[x]=true;
				generate(index+1); //递归处理第 index+1 行皇后
				hashTable[x]=false; 
				
			} 
		}
	}
}
赏

谢谢你

扫一扫，分享到微信

微信分享二维码
总访问量: | 总访客:

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

不会写作的摄影师不是一个好的程序员<br><br> 他人依存型外向<br><br>CS 研二在读<br><br>谢谢你来看我的博客<br>