队列

2020-03-29

view times

先进先出

队列是典型的 FIFO 数据结构。插入（insert）操作也称作入队（enqueue），新元素始终被添加在 队列的末尾。删除（delete）操作也被称为出队（dequeue)。你只能移除 第一个元素。

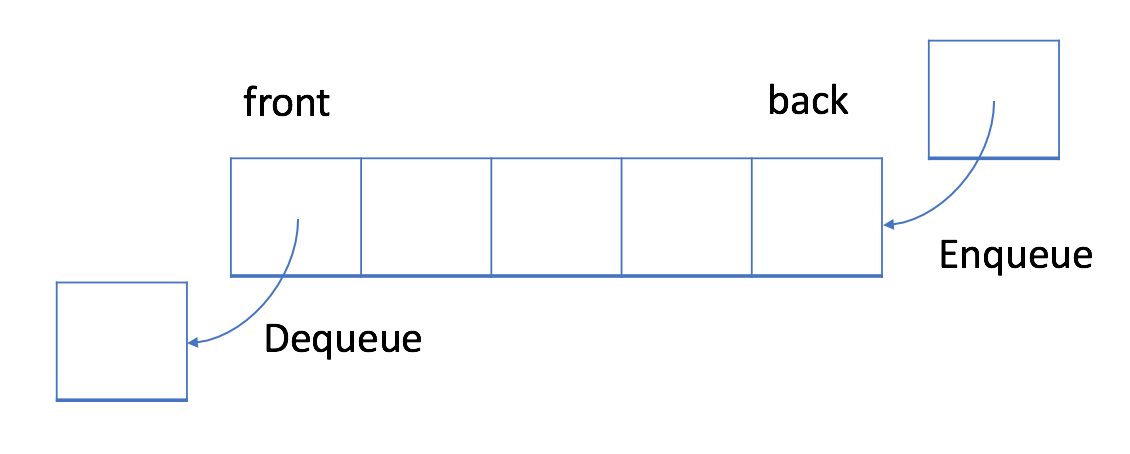
队列实现

为了实现队列，我们可以使用 动态数组 和 指向队列头部的索引。

如上所述，队列应支持两种操作：入队和出队。入队会向队列追加一个新元素，而出队会删除第一个元素。所以我们需要一个索引来指出起点。

#include <iostream>

class MyQueue {
    private:
        // store elements
        vector<int> data;       
        // a pointer to indicate the start position
        int p_start;            
    public:
        MyQueue() {p_start = 0;}
        /** Insert an element into the queue. Return true if the operation is successful. */
        bool enQueue(int x) {
            data.push_back(x);
            return true;
        }
        /** Delete an element from the queue. Return true if the operation is successful. */
        bool deQueue() {
            if (isEmpty()) {
                return false;
            }//出队时注意判断队列是否为空
            p_start++;
            return true;
        };
        /** Get the front item from the queue. */
        int Front() {
            return data[p_start];
        };
        /** Checks whether the queue is empty or not. */
        bool isEmpty()  {
            return p_start >= data.size();
        }
};

int main() {
    MyQueue q;
    q.enQueue(5);
    q.enQueue(3);
    if (!q.isEmpty()) {
        cout << q.Front() << endl;
    }
    q.deQueue();
    if (!q.isEmpty()) {
        cout << q.Front() << endl;
    }
    q.deQueue();
    if (!q.isEmpty()) {
        cout << q.Front() << endl;
    }
}

C++ STL

queue<int> q;
q.push(1);
q.front(); //访问队列的队首元素
q.back();  //访问队列的队尾元素
q.size();  //队列的元素个数
q.pop();   //移除队列的队首元素

循环队列

我们可以使用 固定大小的数组 和 两个指针 来指示起始位置和结束位置。目的是重用我们之前提到的被浪费的存储。

队首指head针和队尾指针tail重合时，队列为空
tail+1 = head 时，队列满

队列和广度优先搜索

1. 结点的处理顺序是什么？

在第一轮中，我们处理根结点。在第二轮中，我们处理根结点旁边的结点；在第三轮中，我们处理距根结点两步的结点；等等等等。

与树的层序遍历类似，越是接近根结点的结点将越早地遍历。

如果在第 k 轮中将结点 X 添加到队列中，则根结点与 X 之间的最短路径的长度恰好是 k。也就是说，第一次找到目标结点时，你已经处于最短路径中。

2. 队列的入队和出队顺序是什么？

如上面的动画所示，我们首先将根结点排入队列。然后在每一轮中，我们逐个处理已经在队列中的结点，并将所有邻居添加到队列中。值得注意的是，新添加的节点不会立即遍历，而是在下一轮中处理。

结点的处理顺序与它们添加到队列的顺序是 完全相同的顺序，即先进先出（FIFO）。这就是我们在 BFS 中使用队列的原因。

伪代码：

/**
 * Return the length of the shortest path between root and target node.
 */
int BFS(Node root, Node target) {
    Queue<Node> queue;  // store all nodes which are waiting to be processed
    Set<Node> used;     // store all the used nodes
    int step = 0;       // number of steps neeeded from root to current node
    // initialize
    add root to queue;
    add root to used;
    // BFS
    while (queue is not empty) {
        step = step + 1;
        // iterate the nodes which are already in the queue
        int size = queue.size();
        for (int i = 0; i < size; ++i) {
            Node cur = the first node in queue;
            return step if cur is target;
            for (Node next : the neighbors of cur) {
                if (next is not in used) {
                    add next to queue;
                    add next to used;
                }
            }
            remove the first node from queue;
        }
    }
    return -1;          // there is no path from root to target
}

如代码所示，在每一轮中，队列中的结点是 等待处理的结点。
在每个更外一层的 while 循环之后，我们 距离根结点更远一步。变量 step 指示从根结点到我们正在访问的当前结点的距离。

有两种情况不需要使用哈希集：

代码中没有循环，例如，在树遍历中；
希望多次将结点添加到队列中。