LeetCode——二叉树 (更新中)

view times

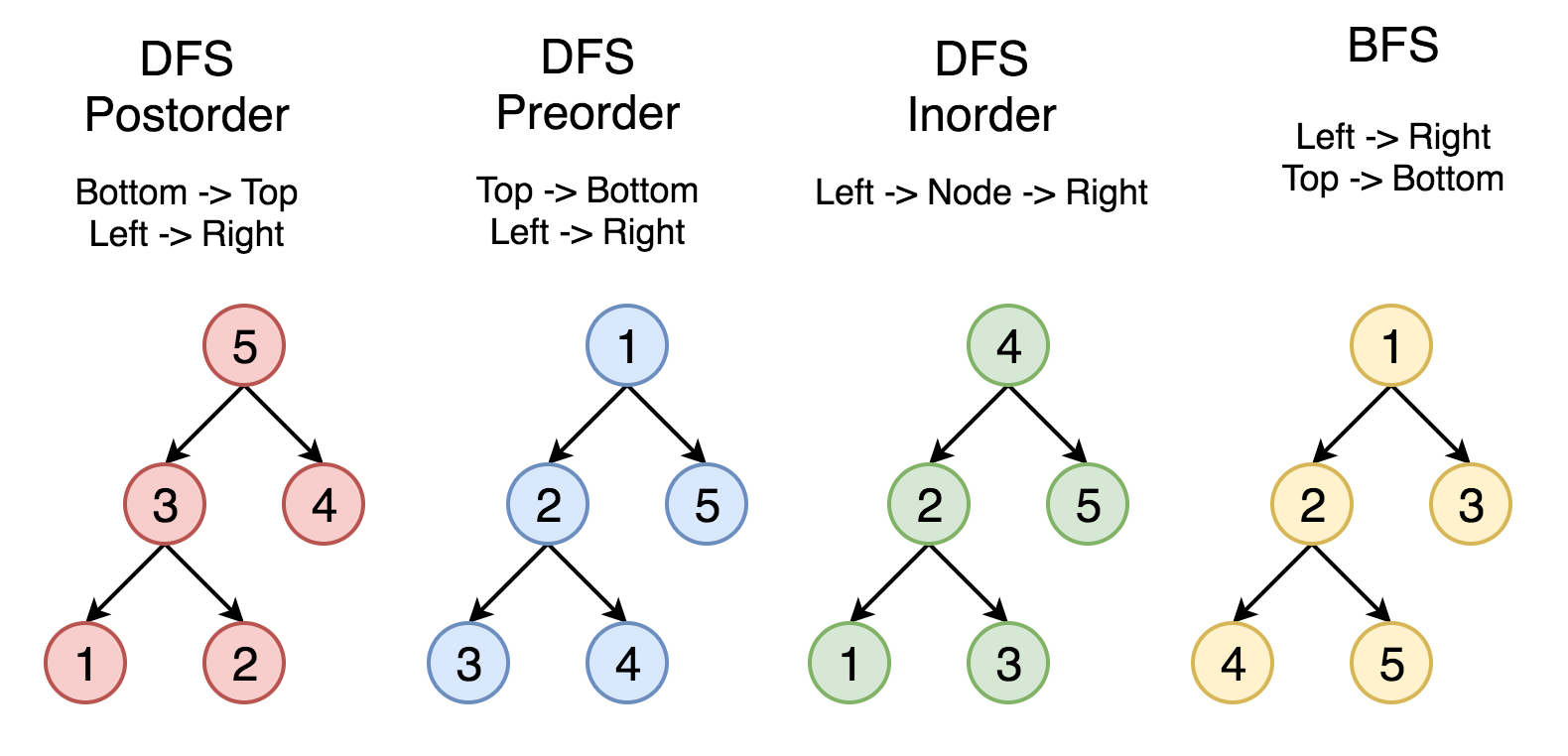
如何遍历一棵树

1. 前序遍历

前序遍历首先访问根节点，然后遍历左子树，最后遍历右子树。

2. 中序遍历

中序遍历是先遍历左子树，然后访问根节点，然后遍历右子树。

通常来说，对于二叉搜索树，我们可以通过中序遍历得到一个递增的有序序列。

3. 后序遍历

后序遍历是先遍历左子树，然后遍历右子树，最后访问树的根节点。

当删除树中的节点时，删除过程将按照后序遍历的顺序进行。 也就是说，当你删除一个节点时，你将首先删除它的左节点和它的右边的节点，然后再删除节点本身。

  • 前、中、后遍历用到了 栈，层序遍历用到了 队列。

    后缀表达式

编写程序来解析后缀表示法更为容易。 这里是一个例子：

image

  • 可以使用中序遍历轻松找出原始表达式。 注意检查操作的优先级。

  • 后序遍历，使用栈来处理表达式会变得更加容易。 每遇到一个操作符，就可以从栈中弹出栈顶的两个元素，计算并将结果返回到栈中。

144 二叉树的前序遍历

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> v;
    vector<int> preorderTraversal(TreeNode* root) {
        if(root==NULL) return v;
        v.push_back(root->val);
        preorderTraversal(root->left);
        preorderTraversal(r
        
        
        
        oot->right);
        
        return v;
    }
};

迭代

利用 深度优先搜索 的思想

在 A 的两棵子树中，遍历完左子树后，再遍历右子树。

从根节点开始，每次迭代弹出当前栈顶元素，并将其孩子节点压入栈中，先压右孩子再压左孩子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> s;
        // 注意 stack 的类型是 TreeNode*
        vector<int> output;
        if(root==NULL)
            return output;
        s.push(root);
        while(!s.empty()){
            TreeNode* node=s.top();
            output.push_back(node->val);
            s.pop();
            if(node->right!=NULL){
                s.push(node->right);
            }if(node->left!=NULL){
                s.push(node->left);
            }
            
        }
        return output;
    }
};
  • 时间复杂度：访问每个节点恰好一次，时间复杂度为 O(N) ，其中 N 是节点的个数，也就是树的大小。
  • 空间复杂度：取决于树的结构，最坏情况存储整棵树，因此空间复杂度是 O(N)。

94 二叉树中序遍历

基于栈的遍历

思路：

  • 每到一个节点 A，因为根的访问在中间，将 A 入栈。然后遍历左子树，接着访问 A，最后遍历右子树。
  • 在访问完 A 后，A 就可以出栈了。因为 A 和其左子树都已经访问完成。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    
    vector<int> inorderTraversal(TreeNode* root) {
        stack<TreeNode*> s;
        vector<int> v;
        TreeNode* curr=root;
        while(curr!=NULL || !s.empty()){
            while(curr!=NULL)
            {
                s.push(curr);
                curr= curr->left;
            }
            curr=s.top();
            s.pop();
            v.push_back(curr->val);
            curr=curr->right;
            
        }
        return v;
    }
};

145 二叉树后序遍历

从根节点开始依次迭代，弹出栈顶元素输出到输出列表中，然后依次压入它的所有孩子节点，按照从上到下、从右至右左顺序依次压入栈中。

因为深度优先搜索后序遍历的顺序是从下到上、从左至右，所以需要将输出列表逆序输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:

    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> s;
        if(root==NULL) return v;
        s.push(root);
        while(!s.empty()){
            TreeNode* node=s.top();
            v.insert(v.begin(),node->val);
            // 在头部插入新元素
            s.pop();
            if(node->left!=NULL)
                s.push(node->left);
            if(node->right!=NULL)
                s.push(node->right);
            
        }
        return v;
    }
};

方法二

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> s;
        TreeNode* last = NULL;
        while (root || !s.empty()) {
            if (root) {
                s.push(root);
                root = root -> left;
            } else {
                TreeNode* node = s.top();
                if (node -> right && last != node -> right) {
                    root = node -> right;
                } else {
                    v.push_back(node -> val);
                    last = node;
                    s.pop();
                }
            }
        }
        return v;
    }
};

102 二叉树的层序遍历

当我们在树中进行 广度优先搜索 时，我们访问的节点的顺序是按照层序遍历顺序的。

使用 队列 来实现广度优先搜索

方法一：递归

  • 输出列表称为 res，当前最高层数就是列表的长度 len(levels)。比较访问节点所在的层次 level 和当前最高层次 res.size() 的大小，如果前者更大就向 res 添加一个空列表。
  • 将当前节点插入到对应层的列表 res[level] 中。
  • 递归非空的孩子节点：helper(node->left / node->right, level + 1)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> res;
    vector<vector<int>> levelOrder(TreeNode* root) {
      
        if(root==NULL) return res;
        helper(root,0);
        return res;
    }
    
    void helper(TreeNode* root,int level){
        if(res.size()==level)       
            res.resize(level+1);    //level表示层数，也对应二维数组的第一层索引，
        res[level].push_back(root->val);
        if(root->left)
            helper(root->left,level+1);
        if(root->right)
            helper(root->right,level+1);
    }
};

方法二：迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> q;
        vector<vector<int>> res;
        if(root==NULL) return res;
        q.push(root);
        while(q.size()){
            vector<int> v;
            int n=q.size();//计算当前层有多少个元素：等于队列的长度。
            for(int i=0;i<n;i++){
            //当前队列中的结点都是同一层的
                TreeNode* node=q.front();
                v.push_back(node->val);
                q.pop();
                if(node->left!=NULL)
                    q.push(node->left);
                if(node->right!=NULL)
                    q.push(node->right);
            }
            res.push_back(v);
        }
        return res;
    }
};

运用递归

许多树问题可以通过递归的方式来解决。 对于每个递归层级，我们只能关注单个节点内的问题，并通过递归调用函数来解决其子节点问题。

“自顶向下” 的解决方案

“自顶向下” 意味着在每个递归层级，我们将首先访问节点来计算一些值，并在递归调用函数时将这些值传递到子节点。 所以 “自顶向下” 的解决方案可以被认为是一种 前序遍历。

  1. return specific value for null node
  2. update the answer if needed // anwer <– params
  3. left_ans = top_down(root.left, left_params) // left_params <– root.val, params
  4. right_ans = top_down(root.right, right_params) >// right_params <– root.val, params
  5. return the answer if needed >// answer <– left_ans, right_ans

二叉树的最大深度

1
2
3
4
5
6
7
8
9
10
11
int answer;		       // don't forget to initialize answer before call maximum_depth
void maximum_depth(TreeNode* root, int depth) {
    if (!root) {
        return;
    }
    if (!root->left && !root->right) {
        answer = max(answer, depth);
    }
    maximum_depth(root->left, depth + 1);
    maximum_depth(root->right, depth + 1);
}

使用“自顶向下”方案的情况

  • 可以确定一些参数，从该节点自身解决出发寻找答案。
  • 可以使用这些参数和节点本身的值来决定什么应该是 传递给它子节点 的参数。

“自底向上” 的解决方案

在每个递归层次上，我们首先对所有子节点递归地调用函数，然后根据返回值和根节点本身的值得到答案。 这个过程可以看作是 后序遍历 的一种。

  1. return specific value for null node
  2. left_ans = bottom_up(root.left) // call function recursively for left child
  3. right_ans = bottom_up(root.right) // call function recursively for right child
  4. return answers // answer <– left_ans, right_ans, root.val

二叉树的最大深度

1
2
3
4
5
6
7
8
int maximum_depth(TreeNode* root) {
	if (!root) {
		return 0;                                 // return 0 for null node
	}
	int left_depth = maximum_depth(root->left);
	int right_depth = maximum_depth(root->right);
	return max(left_depth, right_depth) + 1;	  // return depth of the subtree rooted at root
}

使用“自底向上”方案的情况

  • 对于树中的任意一个节点，如果知道它 子节点 的答案，我们能计算出该节点的答案。

104 二叉树的最大深度

方法一：BFS

  • 层序遍历二叉树，最大层数就是二叉树的深度
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    int maxDepth(TreeNode *root)
    {
        if(root == NULL)
            return 0;
        
        int res = 0,n;
        queue<TreeNode *> q;
        q.push(root);
        while(!q.empty())
        {
            ++ res;
            n=q.size();
            for(int i = 0; i < n; ++ i)
            {
                TreeNode *p = q.front();
                q.pop();
                
                if(p -> left != NULL)
                    q.push(p -> left);
                if(p -> right != NULL)
                    q.push(p -> right);
            }
        }
        
        return res;
    }

方法二：DFS

双栈法：

  • 一个栈存储结点
  • 一个栈存储当前深度
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    class Solution {
    public:
        int maxDepth(TreeNode* root) {
            if(root==NULL) return 0;
            stack<int> res;
            stack<TreeNode*> s;
            s.push(root);
            res.push(1);
            int dep=0;
            while(!s.empty()){
                TreeNode* node=s.top();
                s.pop();
                int temp=res.top();
                dep=max(dep,temp);
                res.pop();
                if(node->left)
                {
                    s.push(node->left);
                    res.push(temp+1);
                }
                if(node->right)
                {
                    s.push(node->right);
                    res.push(temp+1);
                }
            }
            return dep;
        }
    };

101. 对称二叉树

如果同时满足下面的条件，两个树互为镜像：

  • 它们的两个根结点具有相同的值
  • 每个树的右子树都与另一个树的左子树镜像对称

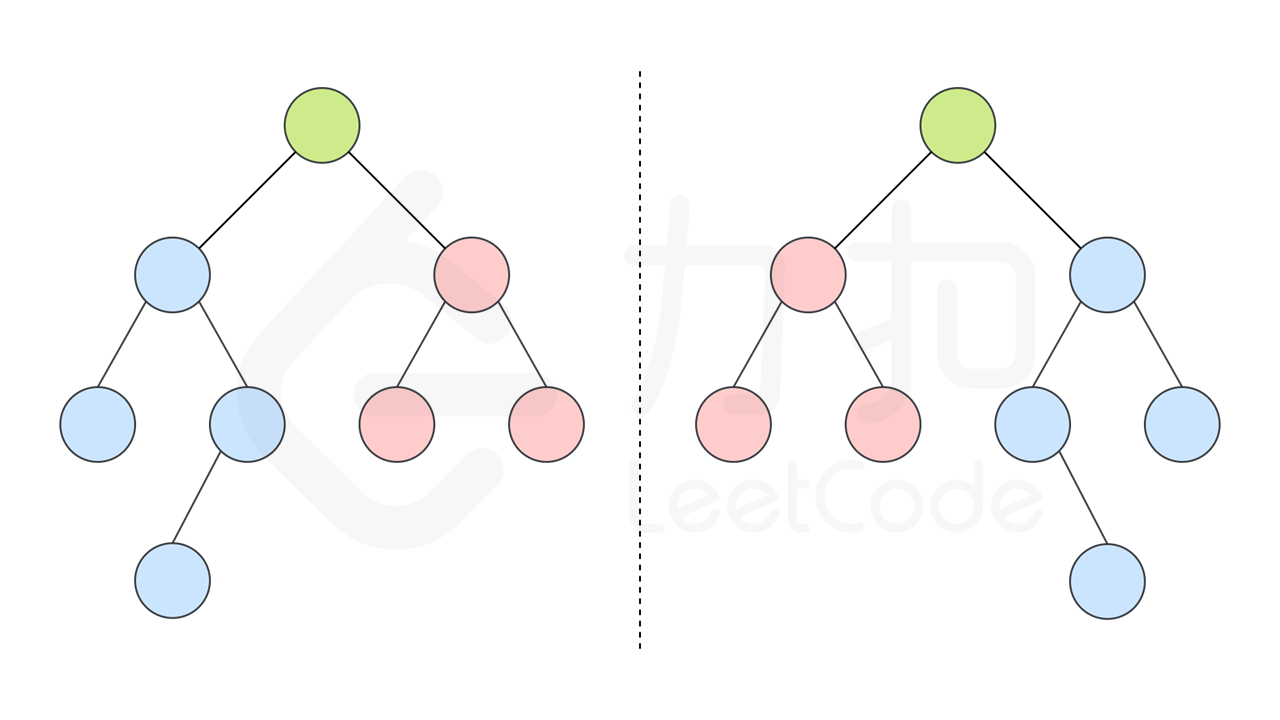
递归

我们可以实现这样一个递归函数，通过「同步移动」两个指针的方法来遍历这棵树，pp 指针和 qq 指针一开始都指向这棵树的根，随后 pp 右移时，qq 左移，pp 左移时，qq 右移。每次检查当前 pp 和 qq 节点的值是否相等，如果相等再判断左右子树是否对称。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return check(root,root);
    }
    
    bool check(TreeNode* p ,TreeNode* q){
        if(!p&&!q)
            return true;
        if(!p||!q)
            return false;
     return (q->val==p->val)&&check(p->left,q->right)&&check(p->right,q->left);
        
    }
};

迭代

引入一个队列，这是把递归程序改写成迭代程序的常用方法。
初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值（队列中每两个连续的结点应该是相等的，而且它们的子树互为镜像），然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时，或者我们检测到树不对称（即从队列中取出两个不相等的连续结点）时，该算法结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    bool check(TreeNode *u, TreeNode *v) {
        queue <TreeNode*> q;
        q.push(u); q.push(v);
        while (!q.empty()) {
            u = q.front(); q.pop();
            v = q.front(); q.pop();
            //注意下面条件的判断
            if (!u && !v) continue;
            if ((!u || !v) || (u->val != v->val)) return false;

            q.push(u->left); 
            q.push(v->right);

            q.push(u->right); 
            q.push(v->left);
        }
        return true;
    }

    bool isSymmetric(TreeNode* root) {
        return check(root, root);
    }
};

112 路径总和

递归

观察要求我们完成的函数，我们可以归纳出它的功能：询问是否存在从当前节点 root 到叶子节点的路径，满足其路径和为 sum。

假定从根节点到当前节点的值之和为 val，我们可以将这个大问题转化为一个小问题：是否存在从当前节点的子节点到叶子的路径，满足其路径和为 sum - val。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int sum) {
        if(!root)
            return false;
        //叶子节点
        if(!root->left && !root->right)
            return sum==root->val;
        return hasPathSum(root->left,sum - root->val)||hasPathSum(root->right,sum - root->val);
    }
};

广度优先搜索

使用广度优先搜索的方式，记录从根节点到当前节点的路径和，以防止重复计算。

这样我们使用两个队列，分别存储将要遍历的节点，以及根节点到这些节点的路径和即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int sum) {
        queue<TreeNode*> q;
        queue<int> qval;
        if(!root)
            return false;
        q.push(root);
        qval.push(root->val);
        while(q.size()){
            TreeNode* node=q.front();
            int val=qval.front();
            q.pop(); qval.pop();
            if(!node->left && !node->right){
                if(sum==val)
                    return true;
                continue;
            }
            if(node->left)
            {
                q.push(node->left);
                qval.push(val+node->left->val);
            }
            if(node->right)
            {
                q.push(node->right);
                qval.push(val+node->right->val);
            }
        }
        return false;
    }
    
};

106 从中序与后序遍历序列构造二叉树

我们可以发现后序遍历的数组最后一个元素代表的即为根节点。知道这个性质后，我们可以利用已知的根节点信息在中序遍历的数组中找到根节点所在的下标，然后根据其将中序遍历的数组分成左右两部分，左边部分即左子树，右边部分为右子树，针对每个部分可以用同样的方法继续递归下去构造。

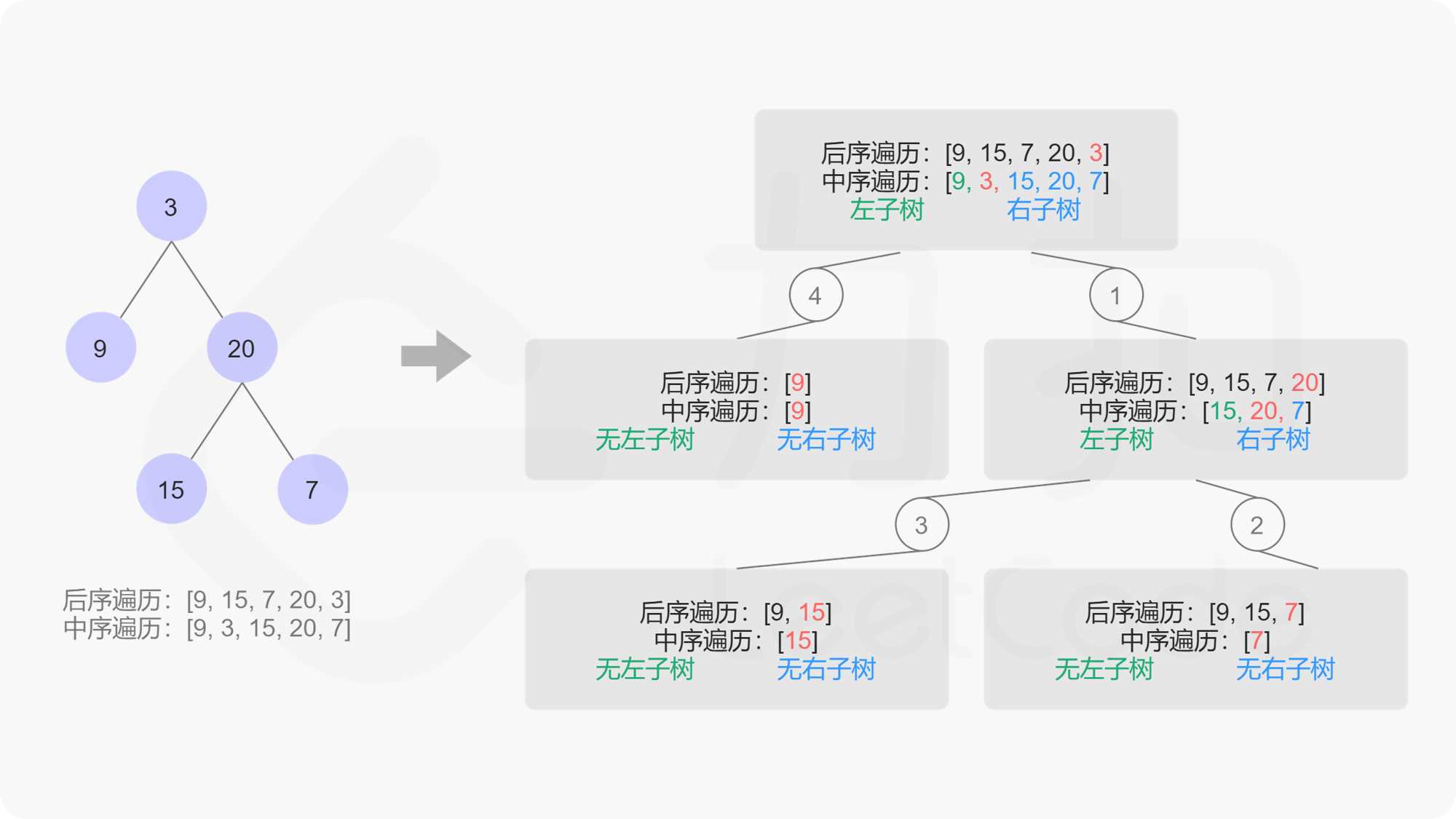
  • 为了高效查找根节点元素在中序遍历数组中的下标，我们选择创建哈希表来存储中序序列，即建立一个（元素，下标）键值对的哈希表。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    unordered_map<int,int> m;
    int post_end;
public:
    
    TreeNode* helper(int left,int right,vector<int>& inorder, vector<int>& postorder )
    {
        if(left>right)
            return nullptr;
        int rootval=postorder[post_end];
        TreeNode* root = new TreeNode(rootval);
        post_end--;
        int mid=m[rootval];
        
        root->right=helper(mid+1,right,inorder,postorder);
        root->left=helper(left,mid-1,inorder,postorder);
        
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        // if(!inorder.size()||!postorder.size())
        //     return nullptr;
        post_end=(int)postorder.size()-1;
        int n=(int)inorder.size();
        int in_start=0;
        for(int i=0;i<n;i++){
            m[inorder[i]]=in_start++;
        }
        return helper(0,n-1,inorder, postorder);
    }
};

105. 从前序与中序遍历序列构造二叉树

对于任意一颗树而言，前序遍历的形式总是

[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
即根节点总是前序遍历中的第一个节点。

而中序遍历的形式总是:

[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]

初始时左子树的

  • 左子树的根节点是前序遍历中当前根节点的下一个元素。
  • 右子树的根节点是前序遍历中当前根节点加上左子树的元素个数再加一。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int,int> m;
    int start;
    TreeNode* helper(int pre_start,int in_start,int in_end,vector<int>& preorder, vector<int>& inorder){
        if(pre_start>preorder.size()||in_start>in_end)
            return nullptr;
        int root_val = preorder[pre_start];
        int mid = m[root_val];
        TreeNode* root = new TreeNode(root_val);
        root->left=helper(pre_start+1,in_start,mid-1,preorder,inorder);
        root->right=helper(pre_start+mid-in_start+1,mid+1,in_end,preorder,inorder);
        //先构建左子树或者右子树都行
        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        start=0;
        int n=inorder.size();
        for(int i=0;i<n;i++)
            m[inorder[i]]=i;
        return helper(0,0,n-1,preorder,inorder);
    }
};

扫一扫，分享到微信

微信分享二维码
总访问量: | 总访客:

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

不会写作的摄影师不是一个好的程序员<br><br> 他人依存型外向<br><br>CS 研二在读<br><br>谢谢你来看我的博客<br>