LeetCode——链表 (更新中)

2021-02-26

view 25 times

单链表

链表定义

定义一个单链表:

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};

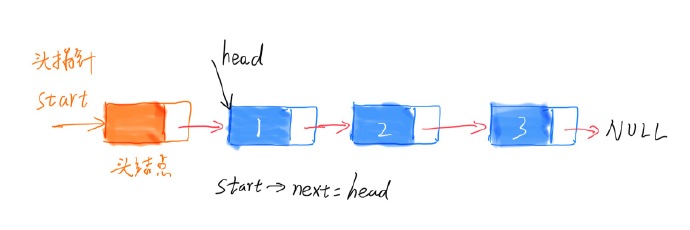
为了统一删除操作，可以手动给链表加一个空的头结点

1	ListNode* start = sas;

让我们从一个经典问题开始：

给定一个链表，判断链表中是否有环。

可以使用哈希表解决。但是，使用双指针技巧有一个更有效的解决方案。。

我们在链表中使用两个速度不同的指针时会遇到的情况：

如果没有环，快指针将停在链表的末尾。
如果有环，快指针最终将与慢指针相遇。

一个安全的选择是每次移动慢指针一步，而移动快指针两步。每一次迭代，快速指针将额外移动一步。如果环的长度为 M，经过 M 次迭代后，快指针肯定会多绕环一周，并赶上慢指针。

problem 141 环形链表

双指针

算法

通过使用具有不同速度的快、慢两个指针遍历链表，空间复杂度可以被降低至 O(1)。慢指针每次移动一步，而快指针每次移动两步。

如果链表中不存在环，最终快指针将会最先到达尾部，此时我们可以返回 false。
如果链表中存在环，则

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head) {
	if (head == NULL || head->next == NULL) {
        return false;
    }
    struct ListNode* slow = head;
    struct ListNode* fast = head->next;
    while(slow!=fast){
    	if(fast==NULL||fast->next==NULL)
    		return false;
    	slow = slow->next;
    	fast = fast->next->next; 
		
	}
	return true;
    
}

problem 142 环形链表 II

To understand this solution, you just need to ask yourself these question.

Assume the distance from head to the start of the loop is x1
the distance from the start of the loop to the point fast and slow meet is x2

the distance from the point fast and slow meet to the start of the loop is x3

What is the distance fast moved? What is the distance slow moved? And their relationship?

x1 + x2 + x3 + x2
x1 + x2
x1 + x2 + x3 + x2 = 2 (x1 + x2)

Thus x1 = x3

struct ListNode *detectCycle(struct ListNode *head) {
    if(head==NULL||head->next==NULL)
		return NULL;
	// 快慢结点起始点一样
	struct ListNode* slow=head;
	struct ListNode* fast=head;
	int f=0;
	while(fast!=NULL&&fast->next!=NULL){
		slow = slow->next;
		fast = fast->next->next;
		if(slow==fast){
            f=1;
            break;
        }
		
		
	} 
	if(f){
		slow = head;
		while(slow!=fast){
			slow = slow->next;
			fast = fast->next;
		}
		return slow;
	}
	return NULL;
}

problem 707 设计链表

有一个空的头结点

typedef struct node{
	int val;
	struct node* next;
	
} MyLinkedList;

/** Initialize your data structure here. */

MyLinkedList* myLinkedListCreate() {
    MyLinkedList *head = (MyLinkedList *)calloc(1,sizeof(MyLinkedList));
    head->next=NULL;
    return head;
}

/** Get the value of the index-th node in the linked list. If the index is invalid, return -1. */
int myLinkedListGet(MyLinkedList* obj, int index) {
	if(index<0)
		return -1;
	int i=0;
	MyLinkedList* p=obj->next;
	while(p!=NULL){ 
		if(i==index)
			return p->val;
			
		p=p->next;
		i++;
	}

	return -1;
}

/** Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list. */
void myLinkedListAddAtHead(MyLinkedList* obj, int val) {
	MyLinkedList* newnode;
	newnode = (MyLinkedList*)malloc(sizeof(MyLinkedList));
	newnode->val = val;
	newnode->next = obj->next;
	obj->next = newnode;
  
}

/** Append a node of value val to the last element of the linked list. */
void myLinkedListAddAtTail(MyLinkedList* obj, int val) {
	MyLinkedList* newnode;
	newnode = (MyLinkedList*)malloc(sizeof(MyLinkedList));
	newnode->val = val;
	newnode->next = NULL;
	
	while(obj->next!=NULL)
		obj = obj->next;
	
	obj->next = newnode;
  
}

/** Add a node of value val before the index-th node in the linked list. If index equals to the length of linked list, the node will be appended to the end of linked list. If index is greater than the length, the node will not be inserted. */
void myLinkedListAddAtIndex(MyLinkedList* obj, int index, int val) {
	if(index<0) return myLinkedListAddAtHead(obj, val); ;
	MyLinkedList* newnode;
	newnode = (MyLinkedList*)malloc(sizeof(MyLinkedList));
	newnode->val = val;
	int i =0;
	MyLinkedList* p;
	p=obj; 
	while(p!=NULL){
		if(i==index){
			newnode->next = p->next;
			p->next = newnode;
			return ; 
		}
		p = p->next;
		i++;	
	}
  	
}

/** Delete the index-th node in the linked list, if the index is valid. */
void myLinkedListDeleteAtIndex(MyLinkedList* obj, int index) {
	if (index < 0) return;
	MyLinkedList *p,*q;
	p=obj;
	int i=0;
	while(p->next!=NULL){
		if(i==index){
			q=p->next;
			p->next=q->next;
			free(q);
			return;
		}
	p=p->next;
	i++;
		   
   }
  
}

void myLinkedListFree(MyLinkedList* obj) {
	MyLinkedList* p;
	while(obj)
	{
		p=obj;
		obj=obj->next;
		free(p);
    }
    
}
/**
 * Your MyLinkedList struct will be instantiated and called as such:
 * MyLinkedList* obj = myLinkedListCreate();
 * int param_1 = myLinkedListGet(obj, index);
 
 * myLinkedListAddAtHead(obj, val);
 
 * myLinkedListAddAtTail(obj, val);
 
 * myLinkedListAddAtIndex(obj, index, val);
 
 * myLinkedListDeleteAtIndex(obj, index);
 
 * myLinkedListFree(obj);
*/

problem 160 相交链表

注意对相交的理解：
相交不是看值相不相等，而是看两个链表是否公用一个地址。就是指向同一块内存。


struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
	if(headA == NULL||headB == NULL)
		return NULL;
	struct ListNode* a = headA;
	struct ListNode* b = headB;
    while(a!= b){
    	a = a == NULL? headB : a->next;
        b = b == NULL? headA : b->next;  
	}
	return a;
}

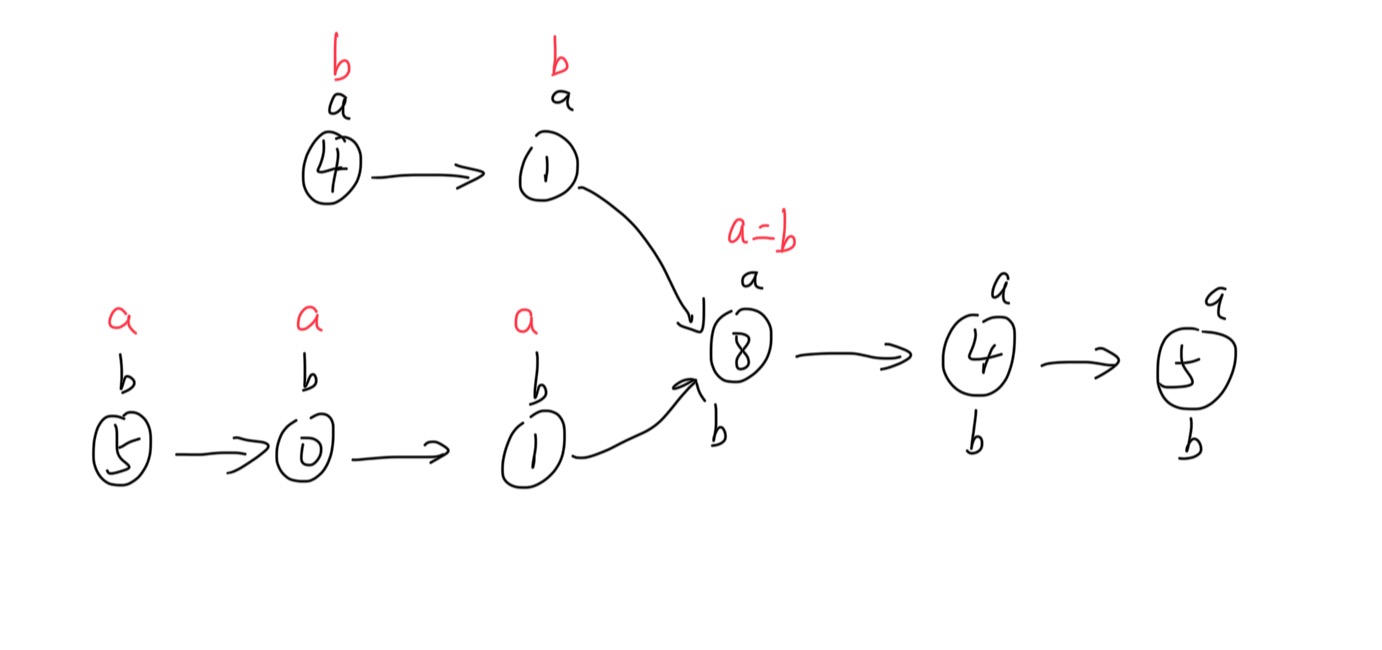
如上图所示，初始时，a 和 b分别指向两个链表 A、B 的头结点，a 比 b 离尾结点快了一个结点，当 a 到达尾结点后指向链表 B 的头结点，当 b 到达尾结点后指向链表 A 的头结点，此时 a 和 b 离尾结点同样距离，两者会在两个链表的相交结点相遇。

若没有相交节点，当两指针值都为 NULL 时，跳出循环。

problem 19 删除链表的倒数第 N 个结点

为了使所有情况的删除操作一致，添加头结点指向原来的第一个结点，头指针指向头结点

方法一：二次遍历

struct ListNode* removeNthFromEnd(struct ListNode* head, int n){
	if(head==NULL||head->next==NULL)
		return NULL;
	struct ListNode* start;
	struct ListNode* first=head;
	start = (struct ListNode*)malloc(sizeof(struct ListNode)); 
	start->next=head;
	int length=0;
	while(first!=NULL){
		length++;
		first=first->next;
	}
	length = length-n;
	first=start;
	while(length){
		length--;
		first=first->next;
	}
	struct ListNode* p=first->next;
	first->next=p->next;
	free(p);
	
	return start->next; 	 

}

复杂度分析

时间复杂度：O(L)，该算法对列表进行了两次遍历，首先计算了列表的长度 L 其次找到第 (L−n) 个结点。操作执行了 2L−n 步，时间复杂度为 O(L)。
空间复杂度：O(1)，我们只用了常量级的额外空间。

方法二：一次遍历

我们可以使用两个指针而不是一个指针。

第一个指针从列表的开头向前移动 n+1 步，而第二个指针将从列表的开头出发。现在，这两个指针被 n 个结点分开。我们通过同时移动两个指针向前来保持这个恒定的间隔，直到第一个指针到达最后一个结点。此时第二个指针将指向从最后一个结点数起的第 n 个结点。

struct ListNode* removeNthFromEnd(struct ListNode* head, int n){
	if(head==NULL||head->next==NULL)
		return NULL;
	struct ListNode* start;
	start = (struct ListNode*)malloc(sizeof(struct ListNode));
	start->next=head;  // 添加空的头结点，使得删除操作一致。
	struct ListNode* slow = start;
	struct ListNode* fast = start;
	
	n+=1;
	while(n){
		fast = fast->next;
		n--;
	}
	while(fast!=NULL){
		fast = fast -> next;
		slow = slow->next; 
	}
	struct ListNode* p=slow->next;
	slow->next=p->next;
	free(p);
	return start->next; 	 

}

复杂度分析

时间复杂度：O(L)，该算法对含有 L 个结点的列表进行了一次遍历。因此时间复杂度为 O(L)。
空间复杂度：O(1)，我们只用了常量级的额外空间。

双指针总结

// Initialize slow & fast pointers
ListNode* slow = head;
ListNode* fast = head;
/**
 * Change this condition to fit specific problem.
 * Attention: remember to avoid null-pointer error
 **/
while (slow && fast && fast->next) {
    slow = slow->next;          // move slow pointer one step each time
    fast = fast->next->next;    // move fast pointer two steps each time
    if (slow == fast) {         // change this condition to fit specific problem
        return true;
    }
}
return false;   // change return value to fit specific problem

在调用 next 字段之前，始终检查节点是否为空。
仔细定义循环的结束条件。

problem 206 反转链表

方法一：迭代

假设存在链表 1 → 2 → 3 → Ø，我们想要把它改成 Ø ← 1 ← 2 ← 3。

在遍历列表时，将当前节点的 next 指针改为指向前一个元素。由于节点没有引用其上一个节点，因此必须事先存储其前一个元素。在更改引用之前，还需要另一个指针来存储下一个节点。不要忘记在最后返回新的头引用！

//迭代方法
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */

struct ListNode* reverseList(struct ListNode* head){
   struct ListNode* prev = NULL;
   struct ListNode* curr = head;
    while(curr!=NULL){
        struct ListNode* temp = curr->next;
        curr->next = prev;
        prev = curr;
        curr = temp;
    }
    return prev;
}

复杂度分析

时间复杂度：O(n)，假设 n 是列表的长度，时间复杂度是 O(n)。
空间复杂度：O(1)。

方法二：递归

递归版本关键在于反向工作。假设列表的其余部分已经被反转，现在该如何反转它前面的部分？

假设列表为：

1	n1 → ··· →n_{k-1} →n_k → n_{k+1}→ ...→n_m → \varnothing

若从节点 $n_{k+1}$ 到 $n_m$ 已经被反转，而我们正处于 $n_{k}$

1	n1 → ··· →n_{k-1} →n_k → n_{k+1} ← ... ←n_m

我们希望 $n_{k+1$ 的下一个节点指向 $n_k$ 。
所以， $n_k.next.next=n_k$

要小心的是 $n_{1}$ 的下一个必须指向 $\varnothing$ 。如果忽略了这一点，链表中可能会产生循环。如果使用大小为 2 的链表测试代码，则可能会捕获此错误。

递归方法一

struct ListNode* reverseList(struct ListNode* head){
	if(head==NULL||head->next==NULL)
		return head;
	struct ListNode* newhead = reverseList(head->next);
	head->next->next = head;
	head->next = NULL;
	
	return newhead;
}

复杂度分析

时间复杂度：O(n)，假设 n 是列表的长度，那么时间复杂度为 O(n)。
空间复杂度：O(n)，由于使用递归，将会使用隐式栈空间。递归深度可能会达到 n 层。

递归方法二

从头结点开始，从左到右，两两反转，同时记录相邻的两个结点，head在前，nextnode在后。直到尾结点终止。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        return reverseListInt(head, NULL);
    }
    
    ListNode* reverseListInt(ListNode* head, ListNode* newHead) {
    if (head == NULL)
        return newHead;
    struct ListNode* nextNode = head->next;
    head->next = newHead;
    //尾递归
    return reverseListInt(nextNode, head);
}
};

因为是尾递归，系统可以重用栈中的固定空间，所以空间复杂度较小。

problem 203 移除链表元素

方法一


class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        if(head==nullptr)
            return nullptr;
        ListNode* start = new ListNode(0);
        start->next = head;
        ListNode* first = start;
        while(first->next!=NULL){
	        if(first->next->val==val){
			    ListNode* p=first->next;
			    first->next=p->next;
			    delete p; 
                continue;
		    }
		    first=first->next;
	    }
	return start->next;
    }
};

方法二：递归

Using a recursive method needs more space/memory since it need to build much more stacks on frame.

方法有弊端，没有 free 被删除的结点。

struct ListNode* removeElements(struct ListNode* head, int val){
	if(head==NULL)
		return NULL;
	
    head->next = removeElements(head->next, val);
    return head->val == val ? head->next : head;

}

problem 328 奇偶链表

维护两个指针 odd 和 even 分别指向奇数节点和偶数节点，初始时 odd = head，even = evenHead。通过迭代的方式将奇数节点和偶数节点分离成两个链表，每一步首先更新奇数节点，然后更新偶数节点。

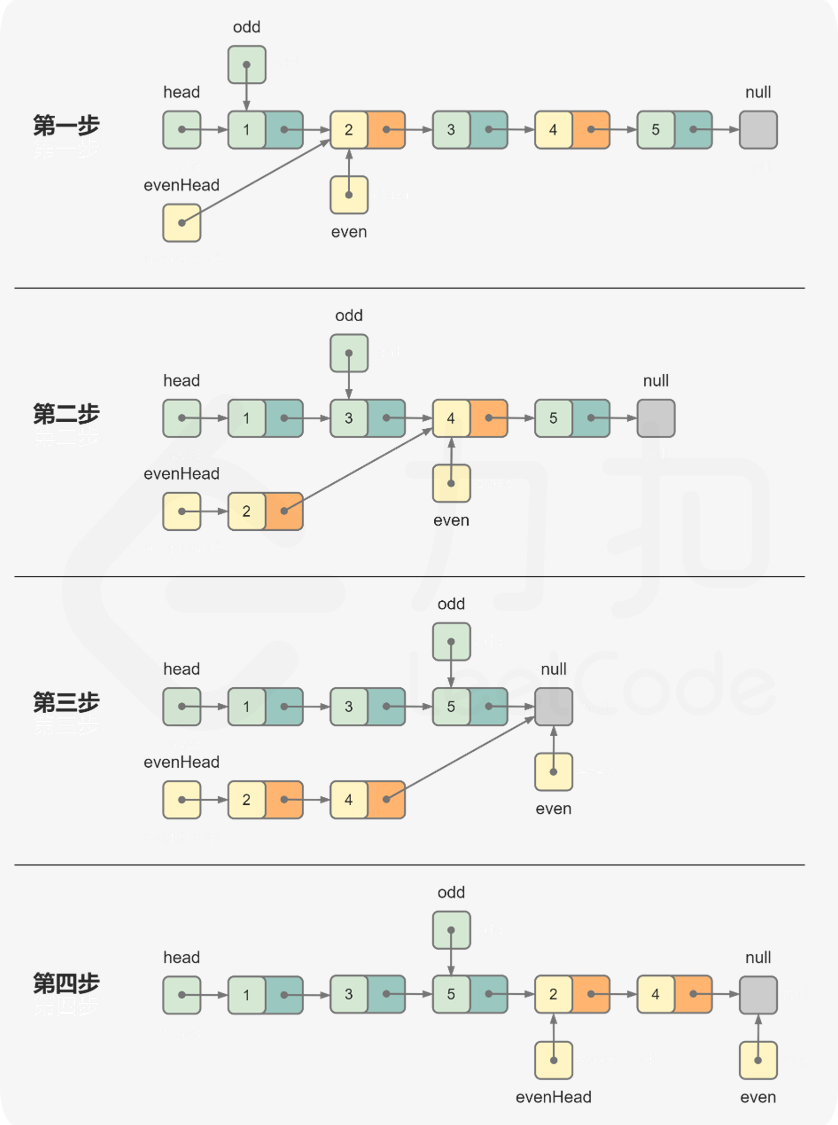
class Solution {
public:
    ListNode* oddEvenList(ListNode* head) {
        if(head==nullptr) return nullptr;
        ListNode* odd = head;  //奇数结点
        ListNode* even = head->next; //偶数结点
        ListNode* tmp = even;
        while(even&&even->next){
            odd->next = even->next;
            odd = odd->next;
            even->next = odd->next;
            even = even->next;
        }
        odd->next = tmp;
        return head;
    }
};

problem 234 回文链表

struct ListNode* reverseList(struct ListNode* head){

	struct ListNode* curr=head;
	struct ListNode* pre=NULL;
	while(curr!=NULL){
		struct ListNode* temp = curr->next;
		curr->next = pre;
		pre=curr;
		curr=temp;
	}
	return pre;
}

bool isPalindrome(struct ListNode* head){
	if(head==NULL||head->next==NULL)
		return true;
	struct ListNode* slow=head;
	struct ListNode* fast=head;
	while(fast!=NULL&&fast->next!=NULL){
		slow=slow->next;
		fast=fast->next->next;
	} 
	if (fast != NULL) { // odd nodes: let right half smaller
        slow = slow->next;
    }
    slow=reverseList(slow);
    fast=head;
    while(slow!=NULL)
    {
    	if(slow->val!=fast->val)
    		return false;
    	slow=slow->next;
    	fast=fast->next;
	}

	return true;
}

我们无法追溯单链表中的前一个结点。因此，我们不仅要存储当前结点，还要存储前一个结点。

双链表

双链表在单链表的基础上增加了一个“prev”指针，用来指向前一个结点。

下面是双链表中结点结构的典型定义：

// Definition for doubly-linked list.
struct DoublyListNode {
    int val;
    DoublyListNode *next, *prev;
    DoublyListNode(int x) : val(x), next(NULL), prev(NULL) {}
};

双链表操作实现

class MyLinkedList {
public:
    struct DoublyListNode {
    int val;
    DoublyListNode *next, *prev;
    DoublyListNode(int x) : val(x), next(NULL), prev(NULL) {}
    };
    /** Initialize your data structure here. */
    MyLinkedList() {
        head = new  DoublyListNode(0);
    }
    
    /** Get the value of the index-th node in the linked list. If the index is invalid, return -1. */
    int get(int index) {
        DoublyListNode* p = head->next;
        while(index--&&p)
            p = p->next;
        if(index&&p==NULL)
            return -1;
        return p->val;
    }
    
    /** Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list. */
    void addAtHead(int val) {
        DoublyListNode* new_node = new DoublyListNode(val);
        new_node->next = head->next;
        if(head->next)
            head->next->prev = new_node;
        new_node->prev = head;
        head->next = new_node;
    }
    
    /** Append a node of value val to the last element of the linked list. */
    void addAtTail(int val) {
        DoublyListNode* new_node = new DoublyListNode(val);
        DoublyListNode* p = head;
        while(p->next)
            p = p->next;
        p->next = new_node;
        new_node->next = NULL;
        new_node->prev = p;
    }
    
    /** Add a node of value val before the index-th node in the linked list. If index equals to the length of linked list, the node will be appended to the end of linked list. If index is greater than the length, the node will not be inserted. */
    void addAtIndex(int index, int val) {
        DoublyListNode* new_node = new DoublyListNode(val);
        DoublyListNode* p =head;
        while(index&&p){
            index--;
            p = p->next;
        }
        if(index==0 && p!=NULL){
            new_node->next = p->next;
            if(p->next)
                p->next->prev = new_node;
            p->next = new_node;
            new_node->prev = p;
        }
    }
    
    /** Delete the index-th node in the linked list, if the index is valid. */
    void deleteAtIndex(int index) {
        DoublyListNode* p = head;
        while(index&&p){
            index--;
            p = p->next;
        }
        if(index==0 && p->next!=NULL){
            DoublyListNode* tmp = p->next;
            p->next = tmp->next;
            if(tmp->next)
                tmp->next->prev = p;
            delete tmp;
        }
    }

    private:
    DoublyListNode* head;
};

/**
 * Your MyLinkedList object will be instantiated and called as such:
 * MyLinkedList* obj = new MyLinkedList();
 * int param_1 = obj->get(index);
 * obj->addAtHead(val);
 * obj->addAtTail(val);
 * obj->addAtIndex(index,val);
 * obj->deleteAtIndex(index);
 */

problem 21 合并两个有序链表

方法 1：递归

我们可以如下递归地定义在两个链表里的 merge 操作（忽略边界情况，比如空链表等）：

\begin{cases} 
list1[0]+merge(list1[1:],list2) & \text {list1[0]<list2[0]} 
\\list2[0]+merge(list1,list2[1:]) & \text{otherwise}
 \end{cases}

也就是说，两个链表头部较小的一个与剩下元素的 merge 操作结果合并。

struct ListNode* mergeTwoLists(struct ListNode* headA, struct ListNode* headB){
	if (headA == NULL) {
            return headB;
        }
        else if (headB == NULL) {
            return headA;
        }
        else if (headA->val < headB->val) {
            headA->next = mergeTwoLists(headA->next, headB);
            return headA;
        }
        else {
            headB->next = mergeTwoLists(headA, headB->next);
            return headB;
        }

}

复杂度分析

时间复杂度：O(n + m)。因为每次调用递归都会去掉 l1 或者 l2 的头元素（直到至少有一个链表为空），函数 mergeTwoList 中只会遍历每个元素一次。所以，时间复杂度与合并后的链表长度为线性关系。
空间复杂度：O(n + m)。调用 mergeTwoLists 退出时 l1 和 l2 中每个元素都一定已经被遍历过了，所以 n +m 个栈帧会消耗 O(n + m) 的空间。

方法2：迭代

设置一个 prehead 结点（虚节点），帮助我们轻松返回合并后新链表的头结点。

循环终止后，l1 和 l2 中最多有一个是非空的。因此（因为输入列表是按有序的），如果其中一个列表是非空的，那么它包含的元素一定大于所有先前合并的元素。这意味着我们可以直接将非空列表连接到已合并列表并返回它。

c 版本

struct ListNode* mergeTwoLists(struct ListNode* headA, struct ListNode* headB){
	struct ListNode* prehead = (struct ListNode*)malloc(sizeof(struct ListNode));
	struct ListNode* prev = prehead;
	while(headA!=NULL && headB!=NULL){
		if(headA->val < headB->val)
		{
			prev->next = headA;
			headA = headA->next;
		}
		else{
			prev->next = headB;
			headB = headB->next; 
		}
		prev = prev->next;
	} 
	 // exactly one of l1 and l2 can be non-null at this point, so connect
        // the non-null list to the end of the merged list.
        prev->next = headA == NULL ? headB : headA;
        
        return prehead->next;
}

c++ 版本

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        ListNode* prehead = new ListNode(-1);
        ListNode* pre = prehead;

        while(l1 && l2){
            if(l1->val<l2->val){
                pre->next=l1;
                l1=l1->next;
            }
            else{
                pre->next=l2;
                l2=l2->next;
            }
            pre = pre->next;
        }
        pre->next = l1==NULL?l2:l1;
        
        return prehead->next;
    }
};

复杂度分析

时间复杂度：O(n + m) 。因为每次循环迭代中，l1 和 l2 只有一个元素会被放进合并链表中， while 循环的次数等于两个链表的总长度。所有其他工作都是常数级别的，所以总的时间复杂度是线性的。
空间复杂度：O(1) 。迭代的过程只会产生几个指针，所以它所需要的空间是常数级别的。
。

problem 876. 链表的中间结点

当用慢指针 slow 遍历列表时，让另一个指针 fast 的速度是它的两倍。

当 fast 到达列表的末尾时，slow 必然位于中间。

struct ListNode* middleNode(struct ListNode* head){
		struct ListNode* slow = head;
		struct ListNode* fast = head;
		while(fast!=NULL && fast->next!=NULL){
			slow=slow->next;
			fast=fast->next->next;
		}
		
		return slow;
}

复杂度分析

时间复杂度：O(N)，其中 N 是给定列表的结点数目。
空间复杂度：O(1)，slow 和 fast 用去的空间。

problem 2. 两数相加

两个链表同时从头开始遍历，注意保留进位。

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode* head = new ListNode(0);
        ListNode* cur = head;
        int tmp=0,sum=0;
        while(l1||l2){
            int n1 = l1?l1->val:0;
            int n2 = l2?l2->val:0;
            sum = n1+n2+tmp;
            tmp = static_cast<int>(sum/10);
            ListNode* new_node = new ListNode(sum%10);
            head->next = new_node;
            if(l1)  l1 = l1->next;
            if(l2)  l2 = l2->next;
            head = head->next;
        }
        if(tmp){
            ListNode* new_node = new ListNode(tmp);
            head->next = new_node;
        }
        return cur->next;
    }
};

problem 61 旋转链表

先找到最后一个结点与头部连成环，然后找到非旋转与旋转部分的分界点，断开环。

class Solution {
public:
    ListNode* rotateRight(ListNode* head, int k) {
        if(head==nullptr||head->next==nullptr)
            return head;
        int n =1;
        ListNode* pre = head;
        while(pre->next){
            pre = pre->next;
            n++;
        }
        pre->next = head;
        k = n-k%n;
        while(k--)
            pre = pre->next;
        head = pre->next;
        pre->next = nullptr;
        return head;
    }
};

146. LRU 缓存机制

我们维护一个有序单链表，越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时，我们从链表头开始顺序遍历链表。

如果此数据之前已经被缓存在链表中了，我们遍历得到这个数据对应的结点，并将其从原来的位置删除，然后再插入到链表的头部。
如果此数据没有在缓存链表中，又可以分为两种情况：
如果此时缓存未满，则将此结点直接插入到链表的头部；
如果此时缓存已满，则链表尾结点删除，将新的数据结点插入链表的头部。

这种基于链表的实现思路，缓存访问的时间复杂度为 O(n)。
引入散列表（Hash table）来记录每个数据的位置，将缓存访问的时间复杂度降到 O(1)。